Various hydrodynamic models have been introduced in order to simulate cerebral haemodynamics. The identification of hydrodynamic models requires an array of signals as input, with the most common of them being arterial blood pressure, intracranial pressure, and cerebral blood flow velocity. Based on these signals, physiological parameters like cerebrovascular resistance and compliances of the cerebrovascular bed and cerebrospinal fluid space can be calculated. In addition, other secondary model-based indices describing cerebrovascular dynamics have been introduced, like the cerebral arterial time constant or critical closing pressure. All of these parameters can be calculated using ICM+.
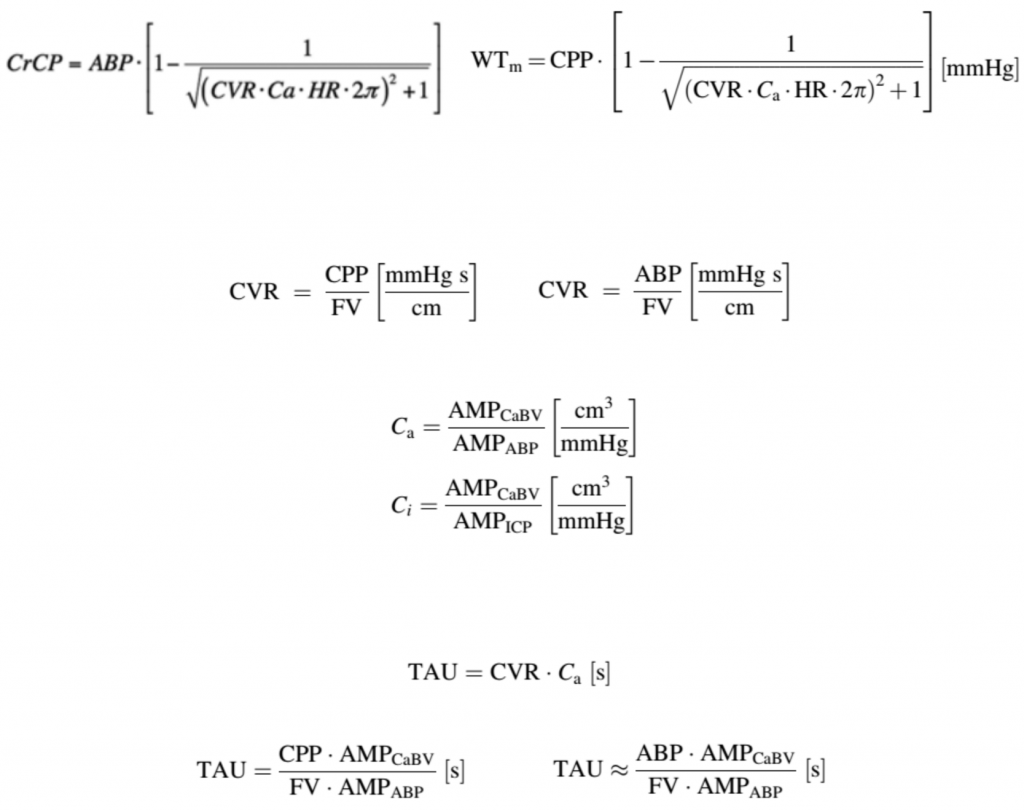
Cerebrosvascular resistance (CVR)
Resistance of the cerebrovascular bed, termed CVR, is the resistance of small cerebral arteries and arterioles. Even though CVR cannot be measured directly, it can be estimated using TCD mean blood flow velocity and mean cerebral perfusion pressure (CPP, calculated as ABP–ICP). In cases where ICP does not change significantly during the measurement time and remains at a physiological level (i.e., much smaller than ABP), CPP can be substituted by ABP.
Cerebrovascular resistance is one of the most important agents of cerebral homeostasis, constituting the functional and anatomical border between two distinctive parts of the cerebrovascular bed: the arterial part with high-pressure flow and the venous part with low pressure. When cerebral autoregulation is intact, CVR is proportional to cerebral perfusion pressure; the upper and lower limits of this proportional relationship denote the corresponding upper and lower limits of cerebral autoregulation.
Compliance of the Cerebrovascular Bed and Compliance of Cerebrospinal Space (Ca and Ci)
Compliance is defined as the change in volume in response to a change in pressure. In a highly compliant system changes of pressure are compensated and do not result in a direct change in volume. There are two main types of compliance, describing the cerebrovascular bed and the cerebrospinal space, respectively. Thus the cerebrovascular arterial compliance (Ca) represents the change of arterial blood volume in response to changes in arterial pressure, whereas the compliance of the cerebrospinal space (Ci) refers to changes of volume of the intracranial space in regards to changes in ICP. Assuming that the parenchymal compartment is nearly incompressible, the changes of volume of the intracranial space through the foramen magnum relate to the volume changes of the vasculature (venous pool) plus displacement of CSF down to the CSF spinal space. In the presented method for calculating Ci the whole cerebrospinal space is treated as one homogenous system, in regards to the CSF pressure and volume relationship. Relative changes in Ca and Ci can be monitored based on a relationship between the pulsatile changes in ABP, ICP, and the cerebral arterial blood volume (CaBV), which is derived from TCD blood flow velocity. AMPCaBV, AMPABP, and AMPICP are the fundamental harmonic amplitudes of the pulse changes of CaBV, ABP, and ICP, respectively, each having been derived using a Fast Fourier Transform of time series of CaBV, ABP, and ICP accordingly.
Cerebral Time Constant (TAU)
The time constant of the cerebrovascular arterial bed (TAU) is a non-invasive TCD-based index indicating how fast arterial blood volume stabilizes after a change in ABP. Put in another way, the time constant is, roughly speaking, the time it takes to fill the arterial bed with blood volume after a sudden change in ABP during one cardiac cycle. TAU is an analog to the time constant of a RC circuit and can be calculated as a product of the CVR and arterial compliance of the cerebrovascular bed (Ca), expressed in time units (seconds). By substituting mean CPP with mean ABP in the above equation, TAU can be estimated non-invasively.
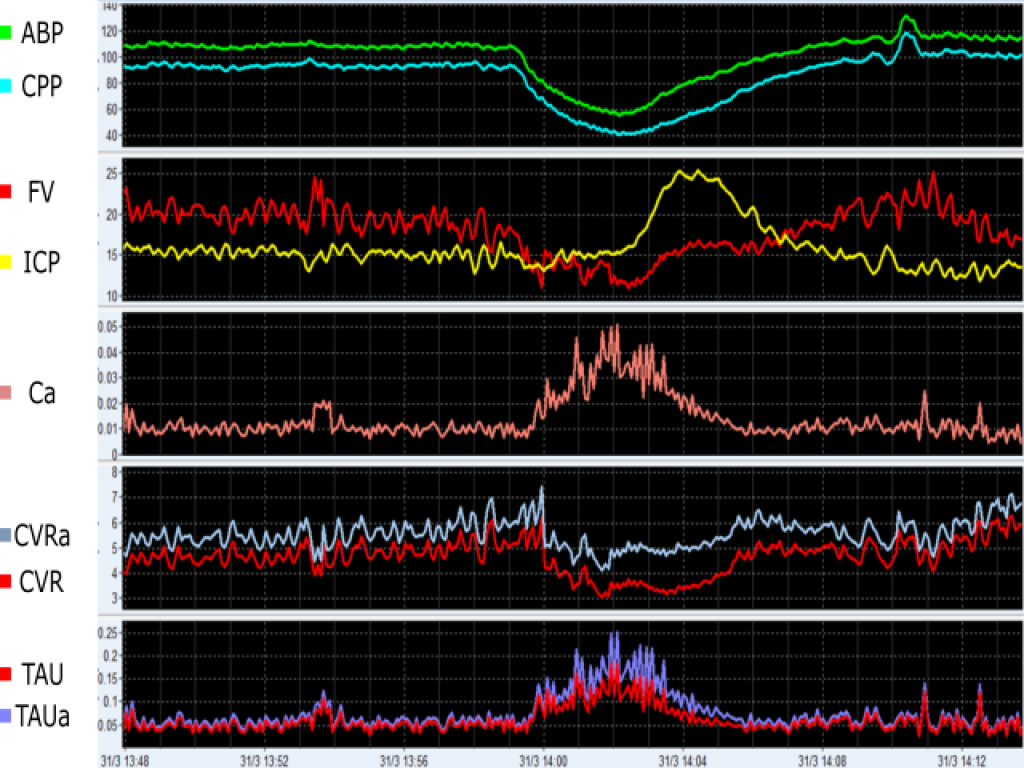
In this example, an event of arterial hypotension leads to decreases in CPP and CVR (indicating vasodilation), which culminates in ICP, Ca and TAU augmentations. ABP (mmHg), arterial blood pressure; CPP (mmHg), cerebral perfusion pressure; ICP (mmHg), intracranial pressure; FV (cm/s), cerebral blood flow velocity; Ca (cm/mmHg), compliance of the cerebral arterial bed; CVR (mmHg/(cm/s)), cerebrovascular resistance calculated using CPP; CVRa (mmHg/(cm/s)), cerebrovascular resistance calculated using ABP; TAU (s), the cerebral time constant calculated using CVR; TAUa (s), and the cerebral time constant calculated using CVRa. View image
Critical Closing Pressure (CrCP)
Critical Closing Pressure (CCP) denotes a lower critical threshold of ABP. When ABP falls below this threshold, the small brain vessels collapse and CBF ceases. The first theoretical model, demonstrating that small vessels collapse when local blood pressure is reduced to a critical value, was developed by Burton in 1951. Since then, CrCP has been studied in various vascular beds and conditions. According to Burton’s model and as a property, CrCP is equal to the sum of ICP and vascular wall tension (WT) representing the active vasomotor tone.

During plateau waves, a vasodilatory cascade promotes a decrease in WT and an increase in cerebral blood volume, leading to ICP and CrCP increases. ABP, arterial blood pressure; ICP, intracranial pressure; CrCP, critical closing pressure; WT, cerebrovascular wall tension. View image